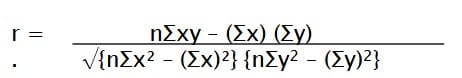Rumusrumus.com kali ini akan membahas perihal pengertian dan rumus hubungan dan bentuk hubungan antara dua variabel beserta klarifikasi mengenai rumus hubungan ganda dan hubungan parsial, untuk lebih jelasnya perihal hubungan yaitu simak klarifikasi dibawah ini.
Pengertian Korelasi
Korelasi atau umumnya disebut koefisien hubungan yaitu nilai yang memperlihatkan kekuatan dan arah hubungan linier antara dua peubah acak
Korelasi Sederhana yaitu suatu Teknik Statistik yang digunakan guna mengukur kekuatan hubungan 2 Variabel dan juga untuk dapat mengetahui bentuk hubungan antara 2 Variabel itu dengan hasil yang sifatnya kuantitatif.
Rumus Korelasi
Koefisien Korelasi Sederhana pada umumnya disebut juga dengan Koefisien Korelasi Pearson alasannya mempunyai rumus perhitungan Koefisien hubungan sederhana dikemukakan oleh Karl Pearson yaitu seseorang hebat Matematika yang berasal dari Inggris. (Rumus ini disebut juga dengan Pearson product moment)
Keterangan Rumus :
n yaitu Banyaknya Pasangan data X dan Y
Σx yaitu Total Jumlah dari Variabel X
Σy yaitu Total Jumlah dari Variabel Y
Σx2 yaitu Kuadrat dari Total Jumlah Variabel X
Σy2 yaitu Kuadrat dari Total Jumlah Variabel Y
Σxy yaitu Hasil Perkalian dari Total Jumlah
Variabel X dan Variabel Y
Bentuk Hubungan Antara 2 Variabel
Korelasi Linear Positif (+1)
- Perubahan Nilai Variabel diikuti perubahan Nilai Variabel yang lainnya secara teratur dengan arah yang sama. Jika Nilai Variabel X mengalami kenaikan, maka Variabel Y juga ikut naik. Jika Nilai Variabel X mengalami penurunan, maka Variabel Y pun ikut turun.
- Jika Nilai Koefisien Korelasi mendekati +1 (positif Satu) berarti pasangan data Variabel X dan Y mempunyai Korelasi Linear Positif yang kuat.
Korelasi Linear Negatif (-1)
- Perubahan Nilai Variabel diikuti perubahan Nilai Variabel yang lainnya secara teratur tetapi dengan arah yang berlawanan. Jika Nilai Variabel X mengalami kenaikan, maka Variabel Y akan turun. Jika Nilai Variabel X turun, maka Nilai Variabel Y mengalami kenaikan.
- Apabila Nilai Koefisien Korelasi mendekati -1 maka hal ini membuktikan pasangan data Variabel X dan Variabel Y mempunyai Korelasi Linear Negatif yang kuat/erat.
Tidak berkolerasi (0)
- Kenaikan Nilai Variabel yang satunya terkadang diikuti dengan penurunan Variabel yang lainnya atau terkadang diikuti dengan kenaikan Variable yang lainnya.Arah hubungannya tidak teratur, searah, dan terkadang berlawanan.
- Apabila Nilai Koefisien Korelasi mendekati 0 (Nol) berarti pasangan data Variabel X dan Y mempunyai hubungan yang sangat lemah atau berkemungkinan tidak berkolerasi
Koefisien hubungan non-parametrik
Koefisien hubungan Pearson yaitu statistik parametrik, dan ia kurang begitu menggambarkan hubungan jikalau perkiraan dasar normalitas suatu data dilanggar. Metode hubungan non-parametrik menyerupai ρ Spearman and τ Kendall mempunyai kegunaan dikala distribusi tidak normal.
Koefisien hubungan non-parametrik masih kurang kuat jikalau disejajarkan dengan metode parametrik jikalau perkiraan normalitas data terpenuhi, tetapi cenderung memperlihatkan hasil distrosi ketika perkiraan tersebut tak terpenuhi.
Korelasi Ganda
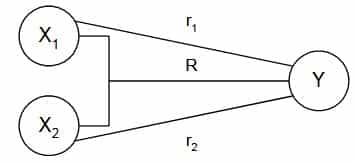
Korelasi pada (multyple correlation) yaitu angka yang memperlihatkan arah dan kuatnya hubungan antara dua variabel secara gotong royong atau lebih dengan variabel yang lainya. Pemahaman perihal hubungan ganda dapat dilihat melalui gambar berikut ini. Simbol hubungan ganda yaitu R
 Keterangan gambar :
Keterangan gambar :
X1 = Kepemimpinan
X2 = Tata Ruang Kantor
Y = Kepuasan Kerja
R = Korelasi Ganda
 Keterangan gambar :
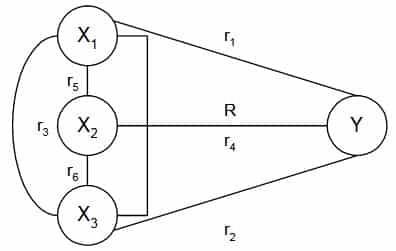
Keterangan gambar :
X1 = Kesejahteraan pegawai
X2 = Hubungan dengan pimpinan
X3 = Pengawasan
Y = Efektivitas kerja
Dari referensi di atas, terlihat bahwa hubungan ganda R, bukan merupakan penjumlahan dari hubungan sederhana yang ada pada setiap variabel (r1-r2-r3). Kaprikornus R (r1+ r2+ r3).
Korelasi ganda merupakan hubungan secara gotong royong antara X1 dengan X2 dan Xn dengan Y. Pada gambar pertama. hubungan ganda merupakan hubungan secara gotong royong antara variabel kepemimpinan, dan tata ruang kantor dengan kepuasan kerja pegawai
Kopula dan korelasi
Banyak yang keliru dan menganggap bahwa isu yang diberikan dari sebuah koefisien hubungan cukup mendefinisikan struktur ketergantungan antara peubah acak.
Untuk mengetahui adanya ketergantungan antara peubah acak harus dipertimbangkan kopula antara keduanya. Koefisien hubungan dapat didefinisikan sebagai struktur ketergantungan hanya pada beberapa kasus, contohnya pada fungsi distribusi kumulatif pada distribusi normal multivariat
Korelasi Parsial
Analisis hubungan parsial digunakan untuk mengetahui hubungan antara dua variabel dimana variabel lainnya yang dianggap besar lengan berkuasa dikendalikan atau dibentuk tetap sebagai variabel kontrol.
Nilai hubungan (r) berkisar antara 1 hingga dengan -1, nilai semakin mendekati 1 atau -1 berarti hubungan antara dua variabel akan semakin kuat, sebaliknya jikalau nilai mendekati 0 berarti hubungan antara dua variabel akan semakin lemah.
Nilai konkret memperlihatkan hubungan searah (X naik maka Y naik) dan nilai negatif memperlihatkan bahwa hubungan terbalik (X naik maka Y turun). Data yang digunakan biasanya berskala interval atau rasio.
Pedoman untuk memperlihatkan interpretasi koefisien hubungan sebagai berikut:
0,00 – 0,199 = sangat rendah
0,20 – 0,399 = rendah
0,40 – 0,599 = sedang
0,60 – 0,799 = kuat
0,80 – 1,000 = sangat kuat
Demikianlah artikel ini, Semoga bermanfaat
Baca Juga :
Sumber https://rumusrumus.com