Rumusrumus.com kali ini akan membahas wacana bilangan komposit mencakup pengertian bilangan komposit dan contoh-contoh bilangan komposit
Pengertian Bilangan Komposit
Bilangan komposit ialah bilangan orisinil lebih dari satu dan bukan merupakan bilangan prima. Bilangan komposit sanggup dinyatakan sebagai faktorisasi bilangan bulat, ataupun hasil perkalian dua bilangan prima atau lebih. Sepuluh bilangan komposit yang pertama yaitu 4,6,8,9,10,12,14,15,16, dan 18. Bisa juga disebut sebagai bilangan yang mempunyai faktor lebih dari dua
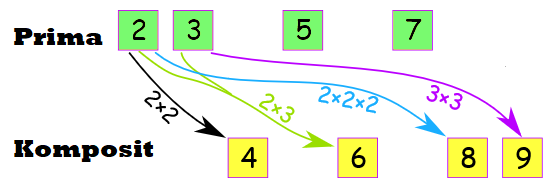
Contoh Bilangan Komposit
Bilangan komposit kurang dari 10
Yaitu: 4, 6, 8 dan 9
Sepuluh bilangan komposit yang pertama
Yaitu: 4, 6, 8, 9, 10, 12, 14, 15, 16 dan 18
Bilangan komposit yang kurang dari 20 (duapuluh)
Yaitu: 4, 6, 8, 9, 10, 12, 14, 15, 16 dan 18
Bilangan komposit sebuah dadu
4 dan 6
Bilangan komposit yang kurang dari 15
4, 6, 8, 9, 10, 12 dan 14
Bilangan komposit yang kurang dari 11
4, 6, 8, 9 dan 10
Bilangan komposit dari 1 hingga 50
Yaitu: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48 dan 49
Lambang Himpunan Bilangan Komposit
Secara umum tak ada lambang khusus pada bilangan komposit, akan tetapi untuk menyatakan suatu bilangan komposit biasa menggunakan simbol aksara ‘K’ (huru k besar).
Himpunan Bilangan Komposit
Himpunan Bilangan komposit kurang dari sepuluh
K = 4, 6, 8, dan 9
artinya anggota himpunan bilangan komposit itu kurang dari 10 yaitu berjumlah 4
Himpunan bilangan komposit yang pertama
K = 4, 6, 8, 9, 10, 12, 14, 15, 16 dan 18
Himpunan Bilangan komposit yang kurang dari duapuluh
K = 4, 6, 8, 9, 10, 12, 14, 15, 16 dan 18
artinya himpunan bilangan komposit yang kurang dari 20 yaitu berjumlah 10.
Cara Mengetahui Bilangan Komposit
Angka 4 termasuk bilangan komposit
Angka 4 sanggup dibagi pada angka 1, 2, dan 4
Dibagi dengan angka 1 (4 : 1 = 4)
Dibagi dengan dirinya sendiri (4 : 4 = 1)
Dibagi dengan bilangan lainnya (4 ÷ 2 = 2) Syarat Komposit
Hingga sanggup diketahui bahwa angka4 didapatkan dari perkalian 2 bilangan prima yaitu 2 × 2
Angka 7 bukan bilangan komposit
Angka 7 cuma sanggup dibagi oleh 1 dan 7, hingga angka 7 hanya mempunyai 2 faktor. Untuk selanjutnya angka 7 yaitu bilangan prima.
Bilangan komposit merupakan bilangan orisinil yang lebih besar dari dan bukan bilangan prima dan disebut juga sebagai bilangan yang mempunyai faktor lebih dari dua. Bilangan ini sanggup dikatakan sebagai faktorisasi bilangan lingkaran dan hasil kali dua bilangan prima atau lebih.
misalnya:
2 x 2 (x2) = 8 ataupun 2x 2 = 4 ataupun 2^3 = 8 ataupun 2^2= 4
3 x 3 x 3 = 27 ataupun 3 x 3 = 9 ataupun 3^3= 27 ataupun 3^2= 9
Pada kesimpulannya ialah apabila ada perkalian 2 bilangan prima ataupun lebih maka bilangan tersebut yaitu bilangan komposit.
Selain bilangan komposit, ada juga bilangan cacah yaitu himpunan bilangan yang terdiri dari bilangan lingkaran dari angka 0 yang bukan bilangan negatif.
Contoh bilangan cacah : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,…
Operasi Penjumlahan pada Bilangan Cacah
yaitu:
Sifat indentitas (contoh : a+0=0+a)
Sifat pengelompokan (contoh (a+b)+c= a(b+c)
Sifat pertukaran, referensi (a+b = b+a)
Operasi Pengurangan Bilangan Cacah
Sifatnya kebalikan dari operasi penjumlahan
contoh a+b=c sama dengan b+c=a (a lebih besar dari b)
a-b=b-a (andai kedua bilangan nilainya sama, a=b)
Operasi Perkalian Bilangan Cacah
Perkalian bilangan cacah itu hasil jumlah yang berulang dari bilangan cacah yang sudah dikalikan
misalnya : 2 x 4 = 4+4 sedangkan 4x 2 = 2+2+2+2
Operasi Pembagian Bilangan Cacah
Operasi pembagian bilangan cacah mempunyai sifat berulang
contoh: 10:2=10-2-2-2-2-2
Hasil pembagian ini ialah jumlah pengulangan angka yang dikurangkan, pada referensi tersebut akibatnya yaitu 5. Di operasi pembagian bilangan cacah tersebut sifat pengelompokan, distributif, pertukaran, dan identitas tak berlaku.
Demikianlah klarifikasi wacana bilangan komposit dan klarifikasi wacana sedikit bilangan ccah semoga lebih gampang memahami bilangan komposit, semoga bermanfaat
Artikel lainya :
Sumber https://rumusrumus.com
