Rumusrumus.com – kali ini akan membahas perihal nilai mutlak, pembahasan mencakup pola soal nilai mutlak dan sifat-sifat pertidaksamaan nilai mutlak biar memahami antara perbedaan nilai mutlak dan ketidaksamaan nilai mutlak
Pada sudut pandang geometri, nilai mutlak dari x ditulis sebagai | x |, yaitu jarak dari x ke 0 pada garis bilangan real. Dikarenakan jarak itu selalu positif atau nol maka nilai mutlak x pun selalu memliki nilai positif ataupun nol untuk setiap x bilangan real.
Secara formal, nilai mutlak x didefinisikan dengan
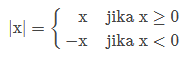
atau bisa ditulis
| x | = -x jikalau x ≥ 0
| x | = -x jikalau x < 0
Definisi diatas bisa di maknai sebagai berikut :
Nilai mutlak bilangan positif ataupun nol ialah bilangan itu sendiri dan nilai mutlak bilangan negatif yaitu lawan dari bilangan tersebut.
Contohnya:
| 7 | = 7 | 0 | = 0 | -4 | = -(-4) = 4
Maka, terperinci bergotong-royong nilai mutlak tiap bilangan real akan selalu mempunyai nilai positif atau nol.
Persamaan √x2=x bernilai benar jika x ≥ 0. Untuk x < 0, maka √x2=−x. Bisa kita tulis
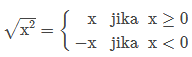
Jika di perhatikan, bentuk diatas sama persis dengan definisi nilai mutlak x. Oleh alasannya itu, pernyataan berikut benar untuk setiap x bilangan real. |x|=√x2 Andai kedua ruas persamaan diatas di kuadratkan bisa didapat |x|2=x2 Persamaan terakhir ini berupa konsep dasar penyelesaian persamaan ataupun pertidaksamaan nilai mutlak dengan cara menguadratkan kedua ruas. Seperti yang di lihat, tanda mutlak akan hilang jikalau dikuadratkan.
Contoh Soal Nilai Mutlak
Contoh 1
Tentukanlah HP |2x – 1| = |x + 4|
Jawaban :
|2x – 1| = |x + 4|
2x – 1 = x + 4 ataupun 2x – 1 = -(x + 4)
x = 5 ataupun 3x = -3
x = 5 ataupun x = -1
Maka, HP = (-1, 5)
Contoh 2
Tentukanlah himpunan penyelesaian |2x – 7| = 3
Jawaban :
|2x – 7| = 3 ( 2x – 7 = 3 ataupun 2x – 7 = -3)
|2x – 7| = 3 ( 2x = 10 ataupun 2x = 4)
|2x – 7| = 3 ( x = 5 ataupun x = 2)
Maka, HP = 2, 5
Contoh 3
Tentukanlah himpunan penyelesaian |4x + 2| ≥ 6
Jawaban :
|4x + 2| ≥ 6 (4x + 2 ≤ -6 atau 4x + 2 ≥ 6)
|4x + 2| ≥ 6 (4x ≤ -8 atau 4x ≥ 4)
|4x + 2| ≥ 6 (x ≤ -2 atau x ≥ 1)
Maka, HP = (x ≤ -2 atau x ≥ 1)
Contoh 4
Tentukan penyelesaian |3x – 2| ≥ |2x + 7|
Jawaban :
|3x – 2| ≥ |2x + 7|
⇔ 3x – 2 ≤ -(2x + 7) ataupun 3x – 2 ≥ 2x + 7
⇔ 5x ≤ -5 ataupun x ≥ 9
⇔ x ≤ -1 atau x ≥ 9
Maka, HP = (x ≤ -1 atau x ≥ 9)
Contoh 5
Tentukanlah himpunan penyelesaian dari |2x – 1| < 7
Jawaban :
|2x – 1| < 7 (-7 < 2x – 1 < 7)
|2x – 1| < 7 (-6 < 2x < 8)
|2x – 1| < 7 (-3 < x < 4)
Maka, HP = (-3 < x < 4)
Sifat Pertidaksamaan nilai mutlak
Mengambil nilai mutlak dari persamaan nilai mutlak pada dasarnya cukup mudah. Dengan mengikuti dua hukum penting sudah bisa memilih nilai mutlaknya. Pada intinya, nilainya akan positif jikalau fungsi dalam tanda mutlak lebih dari nol. Namun akan bernilai negatif jikalau fungsi dalam tanda mutlak kurang dari nol.
Dalam pertidaksamaan nilai mutlak tidak cukup dengan cara begitu. Ada pertidaksamaan aljabar yang ekuivalen dengan pertidaksamaan nilai mutlak. Ataupun bisa disebut sebagai sifat pertidaksamaan nilai mutlak. Sifat inilah yang bisa digunakan untuk memilih himpunan penyelesaian pada soal pertidaksamaan nilai mutlak yang diberikan.
Berikut ini yaitu sifat pertidaksamaan nilai mutlak yang bisa digunakan untuk menuntaskan soal terkait pertidaksmaan nilai mutlak.

Dalam menuntaskan pertidaksamaan nilai mutlak, selain butuh mengetahui sifat yang sudah diberikan di atas, juga diharapkan kemampuan untuk menguasai cara operasi bentuk aljabar Dan cara dasar dalam mengoperasikan bilangan dan variabel.
Demikianlah pembahasan mengenai pola soal nilai mutlak dan sifat-sifat pertidaksamaan nilai mutlak, semoga diberi faham dan bermanfaat
Baca Juga:
Sumber https://rumusrumus.com