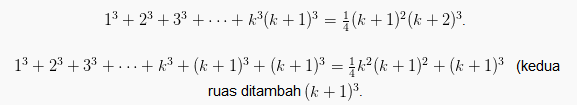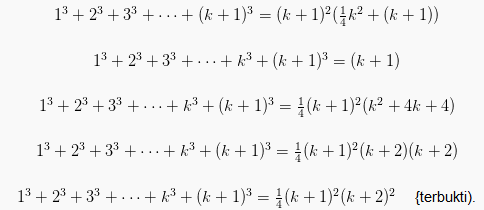Rumusrumus.com kali ini akan membahas wacana pola soal induksi matematika beserta jawabannya dilengkapi juga dengan definisi dan pengertian induksi matematika serta macam -macam langkah menuntaskan induksi matematika.
Induksi Matematika
Induksi matematika adalah bahan yang jadi ekspansi dari kebijaksanaan matematika. Logika matematika mempelajari pernyataan yang dapat bernilai benar maupun salah, ekivalen ataupun ingkaran sebuah pernyataan, dan juga berisi penarikan kesimpulan.
Induksi matematika menjadi salah satu metode pembuktian secara deduktif yang digunakan untuk menandakan suatu pernyataan benar maupun salah. Dimana suatu proses ataupun kegiatan berpikir menarik kesimpulan menurut pada kebenaran pernyataan yang berlaku secara umum hingga pada pernyataan khusus tertentu juga dapat berlaku benar.
Pada induksi matematika, variabel dari suatu perumusan dibuktikan sebagai anggota dari himpunan bilangan yang asli.

Langkah – Langkah Induksi Matematika
Ada tiga langkah dalam induksi matematika yang diharapkan untuk menandakan suatu rumus ataupun pernyataan. yaitu :
- pembuktian pada rumus ataupun pernyataan itu benar untuk n = 1
- pembuktian pada rumus ataupun pernyataan tersebut benar untuk n = k
- Membuktikan pada rumus ataupun pernyataan itu benar untuk n = k + 1
Contoh Soal Induksi Matematika
Buktikan bahwa :
Langkah 1
1 = 1 ( terbukti )
Langkah 2 ( n = k )
Langkah 3 (n=k+1)
Efek Domino
Coba lihat langkah tersebut satu per satu . Mulai dari langkah pertama.
Langkah 1:
Buktikan bahwa Sn ialah benar untuk n=1.
Langkah pertama ini mudah. hanya masukkan nilai n=1 ke persamaan, kemudian hitung deretnya, selesai. Kesimpulannya: S1 yakni benar (Sn benar untuk n=1).
Langkah 2:
Buktikan bahwa benar untuk n=k, andai ia benar juga untuk n=k+1.
Karna pada langkah awal sudah di buktikan bahwa Sn yakni benar untuk n=1, berarti ia benar juga untuk n=2. Kalau Sn benar untuk n=2, maka Sn benar juga untuk n=3. Andai Sn benar untuk n=3, maka Sn benar juga untuk n=4. Dan begitu seterusnya hingga tak terhingga.
Jika klarifikasi di atas masih belum begitu jelas, coba dengan pelan-pelan . Makara bayangkan bergotong-royong pembuktian yang di lakukan pada langkah 1 dan 2 tadi ialah nyatakan dalam dua premis, premis 1 untuk pernyataan pada langkah 2 dan premis 2 untuk pernyataan pada langkah 1. Jadinya begini:
Premis 1: Jika Sn benar untuk n=k, maka Sn benar juga untuk n=k+1
Premis 2: Sn benar untuk n=1
Kesimpulan:
Kalau kita memiliki dua premis menyerupai itu, apa kesimpulan yang dapat diambil? Dikarenakan nilai k=1, berarti k+1 itu ialah 2.
Berarti kesimpulannya yaitu Sn benar juga untuk n=2. Kemudian lanjutkan lagi dengan kesimpulan dan masukkan ke dalam premis 2.
Premis 1: Jika Sn benar untuk n=k, berarti Sn benar juga untuk n=k+1
Premis 2: Sn benar untuk n=2
Kesimpulannya yaitu mudah, ternyata Sn benar untuk n=3. Ini masih dapat di lanjutkan lagi dengan teknik yang sama. Kesimpulan ini di jadikan premis 2.
Premis 1: Andai Sn benar untuk n=k, berarti Sn benar juga untuk n=k+1
Premis 2: Sn benar untuk n=3
Apa kesimpulan dari kedua premis di atas? kesimpulannya yaitu, Sn benar untuk n=4. Bisa lanjutkan proses ini hingga seterunya . Akan tetapi pada suatu titik harus berhenti melaksanakan ini dan mulai berpikir lagi.
Jadi, jika proses ini di lanjutkan, akan mendapat kesimpulan bahwa Sn benar untuk semua n bilangan asli.
Ini sebabnya Induksi Matematika sering juga dikait-kaitkan dengan pengaruh domino. Seperti pengaruh domino, walaupun hanya menjatuhkan domino yang pertama, karenanya seluruh domino tersebut dapat jatuh secara bergantian..
Baca Juga :
Sumber https://rumusrumus.com